Small-World Experiment or Just Six Steps Away off Loneliness…
…”you are not alone
I am here with you
Though you're far away
I am here to stay
***
you are not alone
I am here with you
Though we're far apart
You're always in my heart”…
- Michael Jackson
We are sure that everybody heard this lyrical, romantic song performed by Michael Jackson. But why did the author decide to start this entry with its words? Because the topic of our today’s blog post stirred the association with this particular piece of music in her head.
In truth social networks contributed greatly into ties, connection and communication worldwide, so a rare person now can call him/herself really lonely. In fact, people can’t be happy alone and when there is nobody close by to share your thoughts, woes and joys, you simply enter your G+, Facebook, Twitter or other account and share. Then you get the desired response from people all over the world and it seems to you that our world is not as big as it seems if you can freely send a message to somebody on the other end of the planet and get a reply at a blink of an eye.
This is how people usually use social sites, when they know the members of the group they are in and have similar interests. But have you ever thought how many path-lengths do the information you send needs to reach, say, a completely unknown person living at the other end of your country? Answering this question is the main goal of our blog post. We bet you’ll be surprised how close we are to each other. Plus we would like to discuss what practical significance could this answer have.
Are you ready for a little bit of science? Just read on, we will try to put the information as concise and interesting as possible.
A small-world experiment
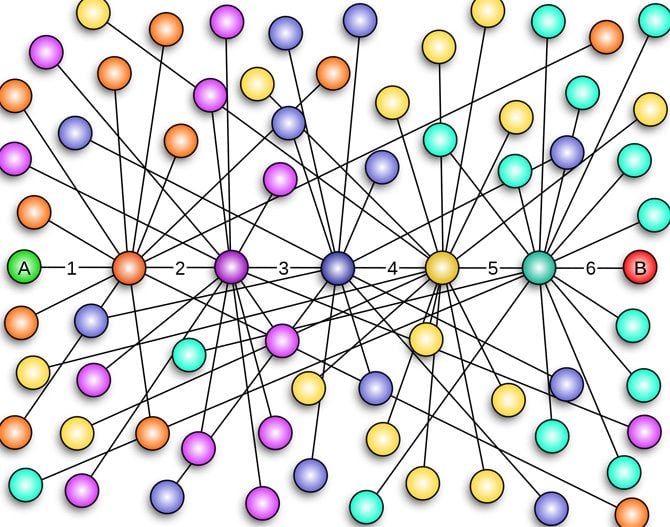
The small-world experiment actually comprised of several experiments conducted by Stanley Milgram and other researchers. Its aim was to examine the average path length for social networks of people in the United States.
What was innovative about this research? The fact that it suggested that human society is a small-world-type network characterized by short path-lengths.
These experiments are often associated with the phrase "six degrees of separation theory", but please note that Milgram never used this term himself.
How the experiment has been carried out?
The idea of Milgram's experiment was born out of the desire to learn more about the probability that two randomly selected people would know each other. This is the first way of looking at the small world problem.
An alternative way of viewing the problem is to imagine the population as a social network and try to find the average path length between any two nodes. The essence of Milgram's experiment was to measure these path lengths by developing a procedure to count the number of ties between any two people.
More about the procedure
The experiment went through several variations, so Milgram typically chose individuals in the U.S. cities of Omaha, Nebraska, and Wichita, Kansas, to be the starting points and Boston, Massachusetts, to be the end point of the correspondence chain. These cities were selected because of the great distance in the United States that separated them both socially and geographically.
The information was initially sent to "randomly" selected individuals in Omaha or Wichita. It included letters, which explained the study's purpose, and basic details on a target contact person in Boston. It also contained a roster on which they could write their own name, as well as business reply cards that were pre-addressed to Harvard.
Upon receiving the invitation to participate, the recipient was asked whether they personally knew the contact person described in the letter. If so, the person was to forward the letter directly to that person. By knowing someone "personally", the scientists meant knowing them on a first-name basis.
However, the more probable case was that the person did not personally know the target. Then, the person was to think of a friend or relative they knew personally who was more likely to know the target. Then the person signed their name on the roster and forwarded the packet. A postcard was mailed to the researchers at Harvard, as well, so that they could track the chain's progression toward the target.
When and if the package eventually reached the contact person in Boston, the researchers could examine the roster to count the number of times it had been forwarded from person to person. Additionally, the incoming postcards helped identify the break point in the chain for packages that never reached the destination.
Attention, please the most interesting part of the experiment – the results!
Shortly after the experiments started, the letters began arriving to the targets and the researchers began receiving postcards from the respondents. Sometimes the packet arrived to the target in one or two hops only, while some chains were composed of nine or ten links. The researches faced a significant problem during the experiment. Very often people refused to pass the letter forward, and thus the chain never reached its destination. In one case, 232 of the 296 letters never reached the destination!
Though, 64 letters eventually did reach the target contact. The average path length among these chains fell around five and a half or six. Hence, the researchers concluded that people in the United States are separated by about six people on average. Although, as we mentioned above, Milgram himself never used the phrase "six degrees of separation", these findings are likely to have contributed to its widespread acceptance.
In an experiment in which 160 letters were mailed out, 24 reached the target in his home in Sharon, Massachusetts. Of those 24, 16 were given to the target person by the same person Milgram calls "Mr. Jacobs", clothing merchant. Of those that reached him at his office, more than half came from two other men.
The researchers used the postcards to qualitatively examine the types of chains that are created. Generally, the package quickly reached a close geographic proximity, but would circle the target almost randomly until it found the target's inner circle of friends. This suggests that participants strongly favored geographic characteristics when choosing an appropriate next person in the chain.
Surely, the Stanley Milgram theory was criticized mostly on his methodology, but we are not going to join the ones who throw the stones into researchers without offering any better solution to the problem. On the contrary, we would like to focus on the useful and practical results of the experiment.
Conclusions
What happens around the small-world question now? It is still a popular research topic today, with many experiments being conducted. For instance, Peter Dodds, Roby Muhamad, and Duncan Watts conducted the first large-scale replication of Milgram's experiment, involving 24,163 e-mail chains and 18 targets around the world. Dodds and others also found that the average chain length was roughly six, even after accounting for attrition. A similar experiment using popular social networking sites as a medium was carried out at Carnegie Mellon University. Its results showed that unfortunately very few messages actually reached their destination.
In 1998, Duncan J. Watts and Steven Strogatz from Cornell University published the first network model on the small-world phenomenon. They showed that networks from both the natural and man-made world, such as the neural network of C. elegans and power grids, exhibit the small-world phenomenon. Watts and Strogatz showed that, beginning with a regular lattice, the addition of a small number of random links reduces the diameter - the longest direct path between any two vertices in the network - from being very long to being very short. The research was originally inspired by Watts' efforts to understand the synchronization of cricket chirps, which show a high degree of coordination over long ranges as though the insects are being guided by an invisible conductor. The mathematical model which Watts and Strogatz developed to explain this phenomenon has since been applied in a wide range of different areas.
"I think I've been contacted by someone from just about every field outside of English literature. I've had letters from mathematicians, physicists, biochemists, neurophysiologists, epidemiologists, economists, sociologists; from people in marketing, information systems, civil engineering, and from a business enterprise that uses the concept of the small world for networking purposes on the Internet." - Duncan J. Watts
Generally, their model corroborated the truth of Mark Granovetter's observation that it is "the strength of weak ties" that holds together a social network. Although the specific model has since been generalized by Jon Kleinberg, it remains a canonical case study in the field of complex networks. In network theory, the idea presented in the small-world network model has been explored quite extensively. Indeed, several classic results in random graph theory show that even networks with no real topological structure exhibit the small-world phenomenon, which mathematically is expressed as the diameter of the network growing with the logarithm of the number of nodes (rather than proportional to the number of nodes, as in the case for a lattice). This result similarly maps onto networks with a power-law degree distribution, such as scale-free networks.
In computer science, the small-world phenomenon, let us call it this way, is used in the development of secure peer-to-peer protocols, novel routing algorithms for the Internet and ad hoc wireless networks, and search algorithms for communication networks of all kinds. So, hopefully now you see that the theory is really applicable at practice and is worth further studying. From our viewpoint, it can contribute greatly into internet marketing. The only question is how you will use this information…
Bye! And stay connected!
Get more to your email
Subscribe to our newsletter and access exclusive content and offers available only to MonsterPost subscribers.




Leave a Reply
You must be logged in to post a comment.